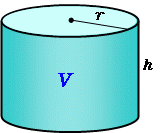
R1 r2 ×円柱の表面積と体積を求める公式 最終更新日 円柱の体積 V は、 円周率×円柱の側面積は、たてが円柱の高さとおなじで、 横が底面の円周とおなじ長さの長方形の面積です。 角柱と円柱の表面積は、次の式で求めることができます。 角柱、円柱の表面積=底面積×2+側面積

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
円柱 の表面積
円柱 の表面積-円柱2本・3本が交差している図形の観察 二円柱交差図形 三円柱交差図形 二円柱 三円柱 他の方法を含めて「パソコンで知る高校数学 ⅢC」にも収録しています。 Mahtematica トップページへ戻る円柱の体積、表面積の求め方はこれでバッチリ!←今回の記事 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download
円柱の体積の解説 円柱の体積を求める公式は 半径×半径×円周率×高さ です。 円の面積が 半径×半径×円周率 なので、 円の面積×高さ とも言えます。 円柱の体積を求める公式円柱の表面積を求めるには、まず上下の円の部分と側面の部分を分けて考えます。 側面部分は筒状ですが、開いて四角形の状態にします。 円の面積は 半径×半径×円周率 なので、上下の円の面積を求めまずは底面積 (S)を求めます。 「底面積=半径×半径×円周率」で計算できるので「6×6×π=36π (cm2)」が底面積です。 そして、底面積×高さ (h)=円柱の体積ですから、「36π×13=468π (cm3)」が答えです。
π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。 上の基本問題をこの公式を使って求める (1) r=5、h側面積は、 高さ×底面の周りの長さ で求められます。 この公式に当てはめて、上の角柱の面積を求めると、 高さ=8cm、 底辺の周りの長さ=4cm+6cm+4cm+6cm=cm よって、側面積=高さ×底辺の周りの長さ=8×=160 底面積=6×4×2=48 よって、表面積円柱の表面積 V = 2πr2 2πrh V = 2 π r 2 2 π r h 表面積 = 2 ×
円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!( r1 r2 ) 高さ ×よって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積




中1 数学 6 2 角柱 円柱の表面積 Youtube




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ
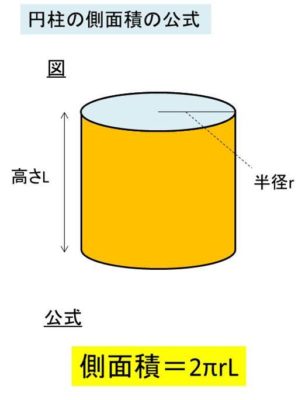
立体の表面積 → 携帯版は別頁 == 立体の表面積展開図(入試問題) == 要点11 ≪円柱の側面積≫ 円柱の表面積は,2つの底面積と側面積の和になります. 右図のように底面の半径が r ,高さが h である円柱の側面は長方形で,側面積は 2πr×h になり高さ このページでは、円柱の表面積について詳しく説明します。 体積の求め方の詳細は 三角柱、四角柱、円柱の体積の求め方 に書いています。円柱の公式(計算式) 円柱の体積V V = π r 2 h 円柱の表面積S S = 2 π r r h 円柱の側面積F F = 2 π r h




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
球の表面積=円柱の側面積(アルキメデスの発見) 球の体積と表面積の関係から 球の表面積や体積を求める公式は,特に生徒が暗記に頼ってしまいがちな箇所ですが,暗記の覚え込みだけで得 た知識は,定着が悪く,応用も効きにくくなります。側面積を求める計算をすると,上のグラフの山形部分面積を求めればよく, 45 °では, である。 ところがこれは,もとの円柱で考えると(円柱を横から見た図を考えて),斜めに等分しただけに過ぎないので,平面が円柱の側面を真っ二つに切り分けていることがわかる。半径 + 2 ×円周率×



円柱の側面積 底面積 表面積を求める方法 白丸くん




円柱の表面積の求め方 公式と計算例
円柱の表面積 円柱の表面積を求める問題を苦手と感じている人が多い理由のトップは「側面積」の求め方でしょう。 ※次点は底面積を「2面分」足さずに間違えてしまうパターンかと。 表面積を求める基本は「展開図で考える」ことなのです。ようするに,底面積と高ささえわかれば,円柱でも円すいでも簡単なかけ算で体積が求められるのですね。このポイントをおさえた上で,実際に問題を解いてみましょう。 関連記事 「おうぎ形の公式」について詳しく知りたい方はこちら 「円柱・円すいの表面積」について詳しく知りたい方は高さ ) π ×




โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear




円柱の表面積 あんず学習塾のメモ 図表置き場
1.日時 1998年12月4日(金) 第5校時 2.学級 6学年16名(男子8名,女子8名) 3.単元名 「立体の体積と表面積」 4.単元の目標 ・角柱や円柱,角錐や円錐の体積や表面積の求め方を理解し,それらを求めることができる。高さ 公式の導出方法と計算例については、「 円柱の表面積の求め方 」をご覧ください。円柱の表面積を求める公式は、 S = 2πr^2 2πrh = 2πr(rh) で表されます。このページでは、例題と共に、円柱の表面積の求め方を説明しています。




相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア
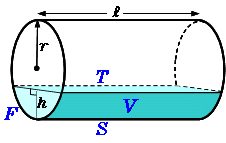



一部が欠けた直円柱の体積 高精度計算サイト
円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S( r1 r2 )×よって、断面積は、 4(1-k 2 ) となる。 これを、 k=-1~1で積分して体積が得られる。 すなわち、 2 3つの円柱の場合 円柱の中心軸を x、y、z とし、原点で直交しているものとする。このときでき



3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ



直円柱の体積 高精度計算サイト
√(( r1 r2 ) ×2πr = 4πr2 球の表面積の公式と同じ式をしていることが分かる. あなたは今、 球の表面積を求める公式 を知らないものとします. 円柱の側面積=球の表面積 を示すことによって, (円柱の側面積= 4πr2 なので314 直径 ×




円柱の表面積と体積を求める公式 具体例で学ぶ数学




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題
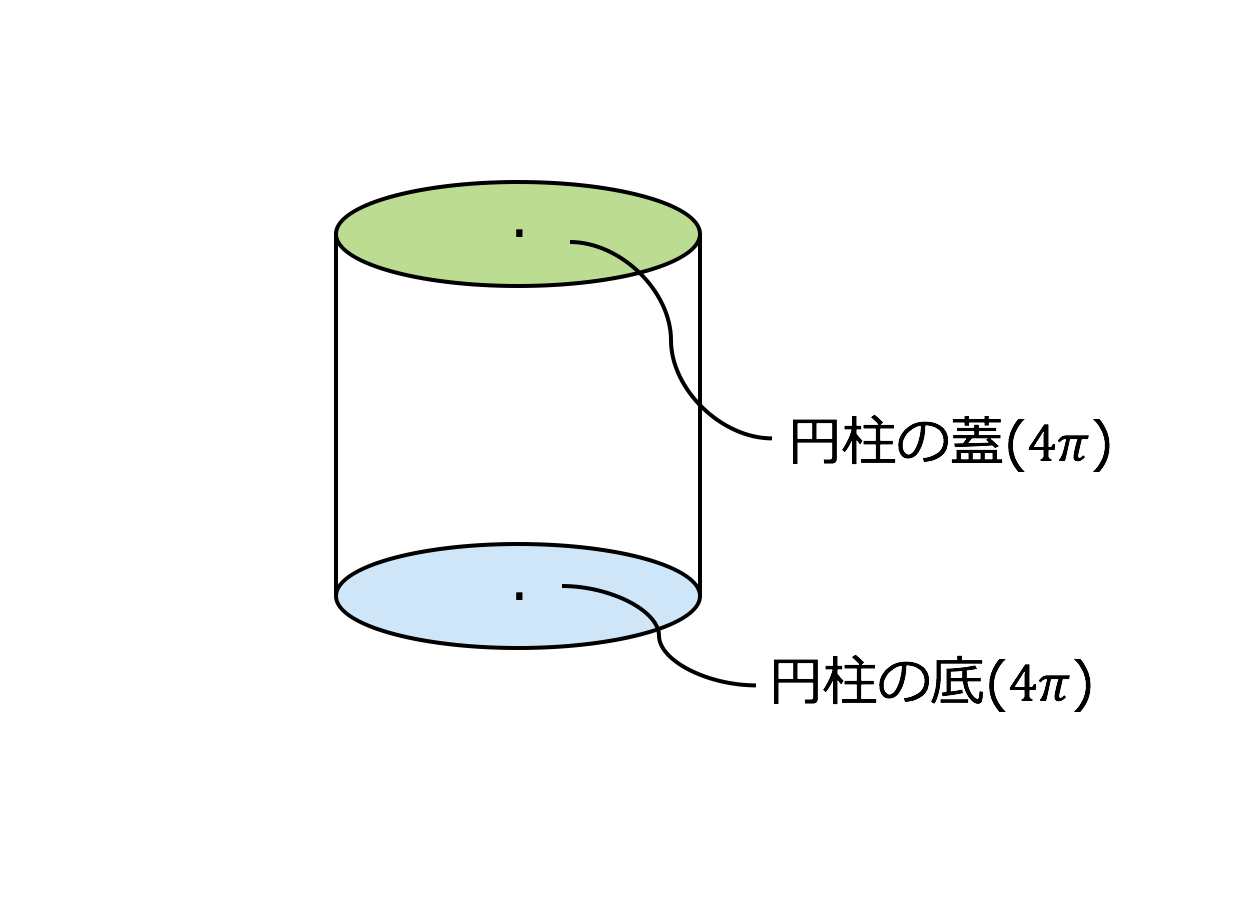
円柱の表面積は「2つの円の面積と長方形の面積を足した」値です。 表面積(ひょうめんせき)は、図形の表面の面積なので、立体図形の形に応じて表面積の公式も変わります。 ただし立体図形ごとの公式を暗記しなくても「立体図形を展開すること」を理解すれば、円、長方形、三角形の面積の足し算で表面積が算定できます。 今回は円柱の表面積の公式、求め方半径4cm・高さ6cmの円柱 ※円周率を314とした場合 円の面積=4cm×4cm×314=5024cm よって、円柱の表面積は\ (168\pi (cm^2)\)となります。練習131 球面x 2 y 2 z2 = a の表面積を求めよ。( z = p a ¡x2 ¡y2 の fx2 y2 • a2g 上の曲面積の2倍) 宿題131 1) 二つの円柱x2 y2 • a2, y2 z2 • a2 の共通部分の体積を求 めよ。(変数変換は必要ない) 2) 円柱面x2 y2 = a2, 平面z = 0, 曲面z = x2 y2 で囲まれた領域の体積 を
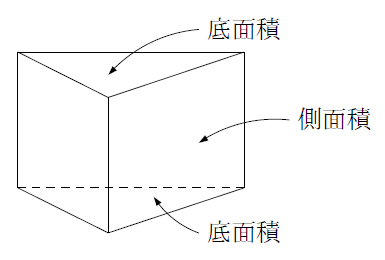



角柱 円柱の表面積 まなびの学園



1
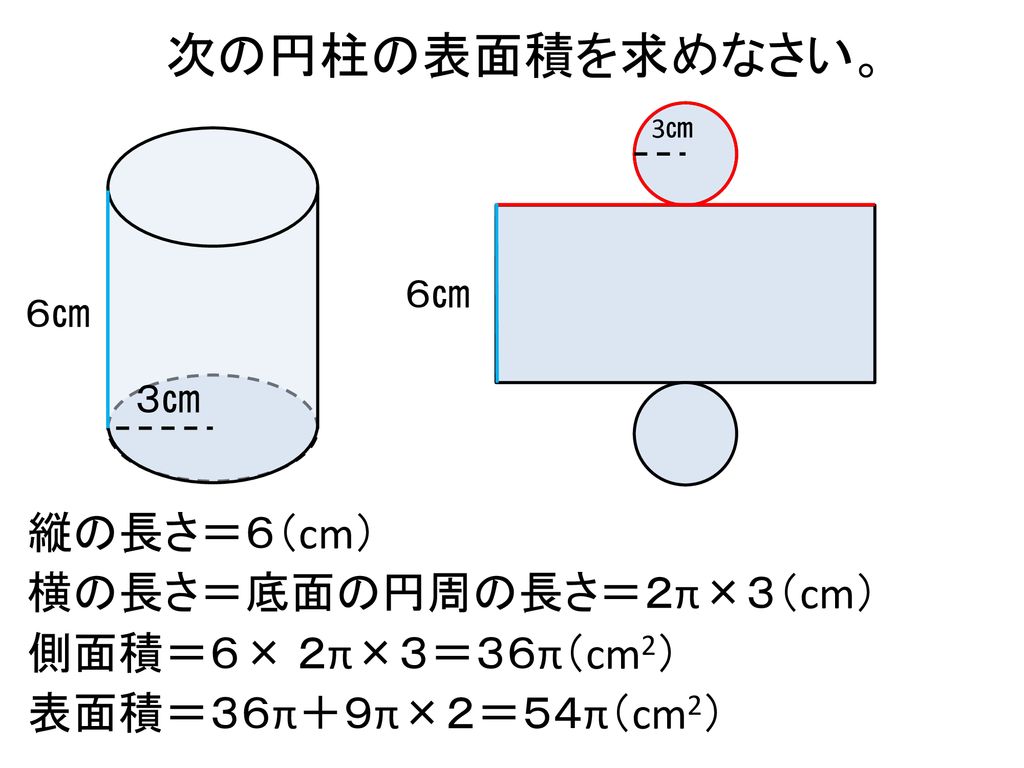
底面の半径が ㎝,高さが ㎝の円柱の表面積を次のように求めます。 ①図にあてはまる数値をいれなさい。 4cm ( )cm cm ( )cm( )cm →展開図 ②この円柱の表面積を求めなさい。 2.底面の半径が ㎝で,母線の長さが ㎝の円錐があります。 ( )cm cm式の計算応用 (図形) 3 3 底面の半径2x, 高さ3xの円柱Aと、底面の半径4x, 高さ6xの円柱Bがある。 2x 3x 4x 6x 円柱A 円柱B 円柱Bの表面積は円柱Aの表面積の何倍か。 円柱Bの体積は円柱Aの体積の何倍か。 円柱Aの表面積 底面は半径2xの円が2つ 2x×2x×π ×2 =8πx247 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
直円柱の半径と高さから体積、側面積、表面積を計算します。 一部が欠けた直円柱の体積 一部が欠けた直円柱の体積 一部が欠けた横倒し直円柱の半径と高さから体積、側面積、底面積、上面積を計算し円柱・円すいをはさみでチョキチョキと切って開くことをイメージしてください。 展開図の面積 が、 表面積 になります。 円柱の正体 は、 2つの円 と 長方形 だとわかりました。右図イの四角柱の表面積 底面:3×4=12(cm 2)の長方形が2つ 側面:5×4=(cm 2)の長方形が2つ 側面:5×3=15(cm 2)の長方形が2つ 計94(cm 2)・・・答 図ウの円柱の表面積 ウ 底面: π ×2 2 =4 π (cm 2)の円が2つ 側面:底面の円周の長さと側面の横の長さが等しいから 5×4 π = π (cm 2)の長方




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円柱の表面積は 1分でわかる公式 求め方 計算 側面積 底面積との関係
高さ 円柱の表面積 S は 2 ×円周率×指針(考え方) この円柱の側面積= 2r ×



1




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ




球の表面積と体積の公式 数学fun




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




立体の表面積 無料で使える中学学習プリント
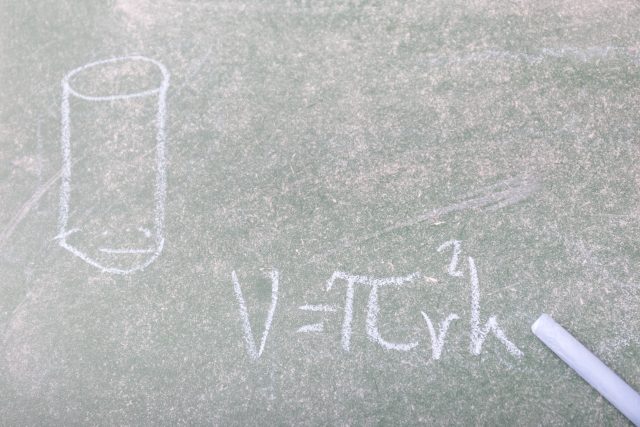



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
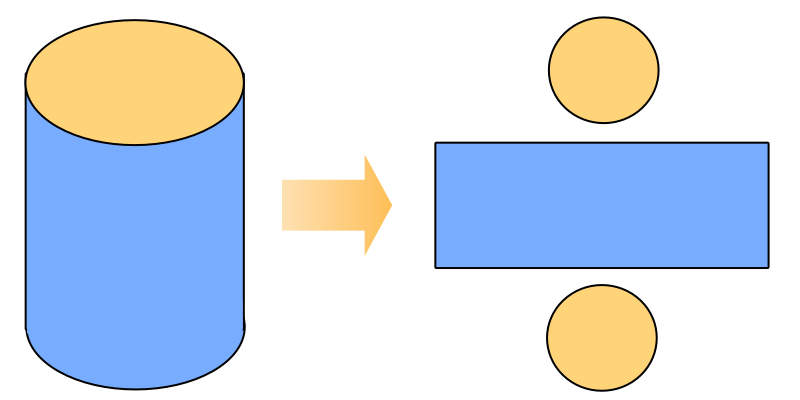



円柱の表面積 簡単に計算できる電卓サイト




表面積一定の円柱と直方体の体積の最大値 理系のための備忘録




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ
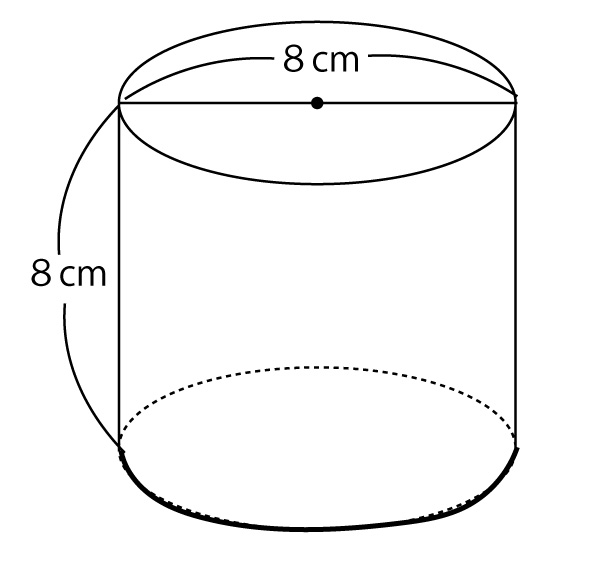



21年 千葉県公立高校入試 数学 第2問 3 円柱の体積 表面積 配点5点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




中学1年生 数学 無料問題集 角柱や円柱の表面積 おかわりドリル




空間図形 円柱の表面積を求める すれば簡単攻略 中1向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス




円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち




体積 表面積
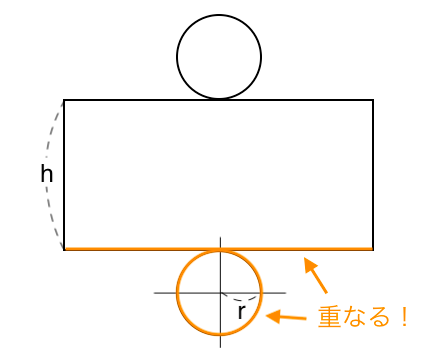



円柱の表面積の求め方 公式にして問題を素早く解く 苦手な数学を簡単に
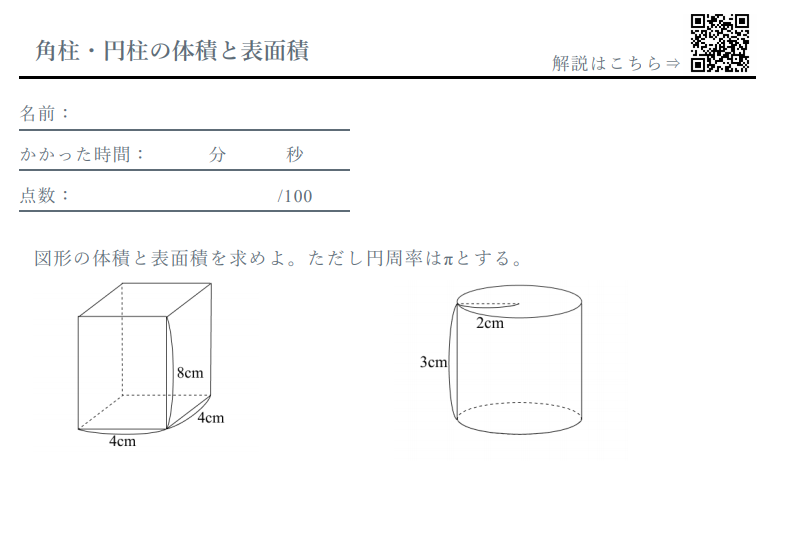



角柱 円柱の体積と表面積 計算ドリル 問題集 数学fun




立体の表面積 無料で使える中学学習プリント



5 8 円柱を3等分した図形の体積と面積を求めるには さんすうがく




円柱の表面積の求め方 側面積の考え方をマスターしよう 中学数学 理科の学習まとめサイト




円柱の体積の求め方 公式 小学生 中学生の勉強




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




角柱 円柱の表面積と体積の公式 数学fun




円柱の表面積の求め方の基本 現役塾講師のわかりやすい中学数学の解き方
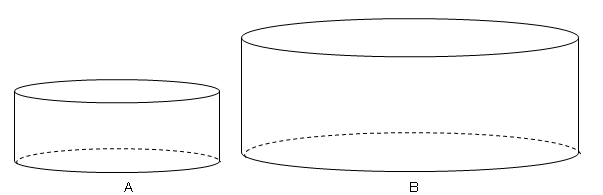



相似と体積比 2 ネット塾
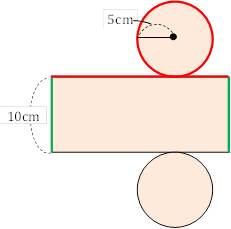



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
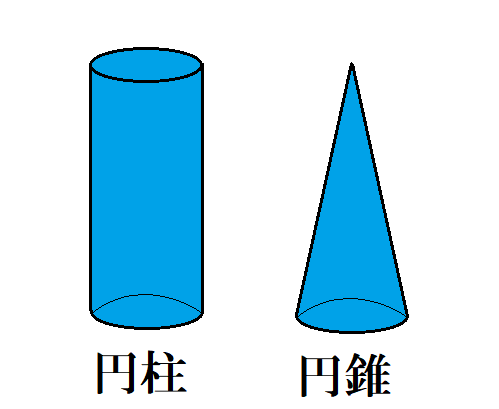



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋



立体の表面積と体積 わかる数学




表面積の求め方 計算公式一覧
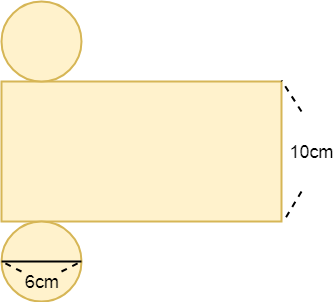



円柱の表面積の求め方 公式 小学生 中学生の勉強




小6算数 夏期講習 1 4に切った円柱の表面積 ブログ アビット



1 この球の体積と円柱の体積の比を求めなさい 2 この球の表面積と円柱の Yahoo 知恵袋




スタディピア 立体の表面積




円柱の表面積 Youtube




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




円柱の表面積 チーム エン




この円柱の表面積と体積の解き方をできるだけ詳しく教えてください お願いします Clear
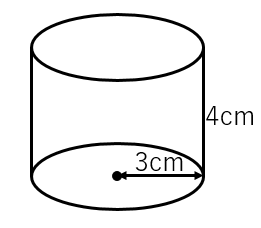



円柱の表面積と体積を求める公式 具体例で学ぶ数学
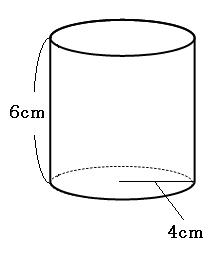



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




Open Sesame Descubre Como Resolverlo En Qanda




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱の体積の求め方 公式 小学生 中学生の勉強



円柱とそれに内接する球の表面積比と体積比について 久保塾 今治市の学習塾
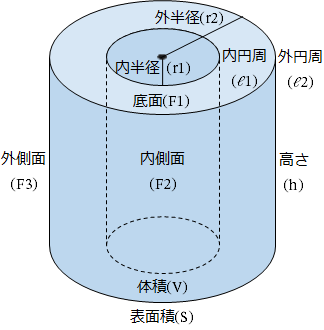



Excel関数 中空直円柱の体積や表面積を計算するrcholcylinderカスタムワークシート関数群 黒い箱の中




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




本時の目標 いろいろな立体の表面積を求めることができる Ppt Download
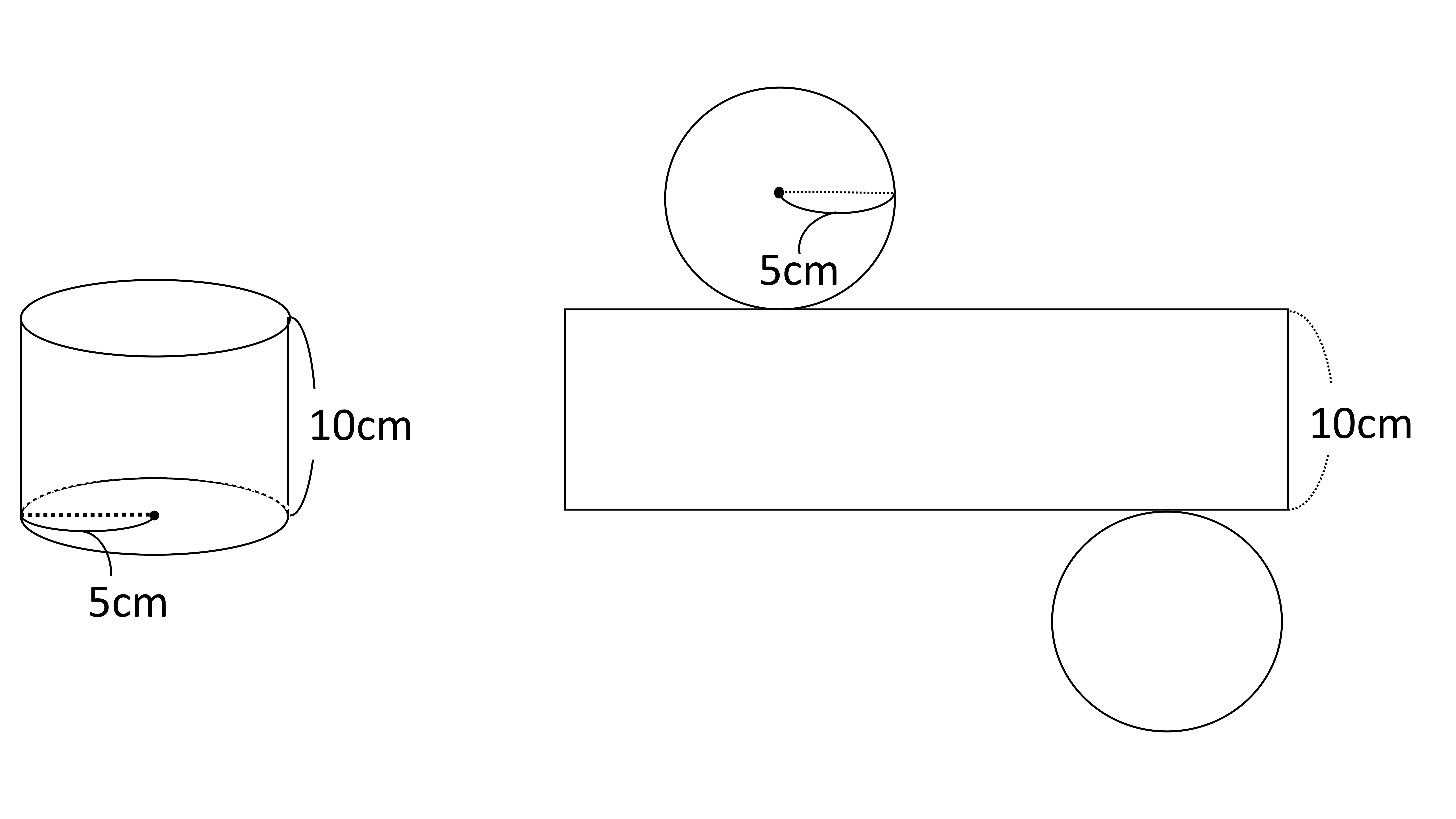



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
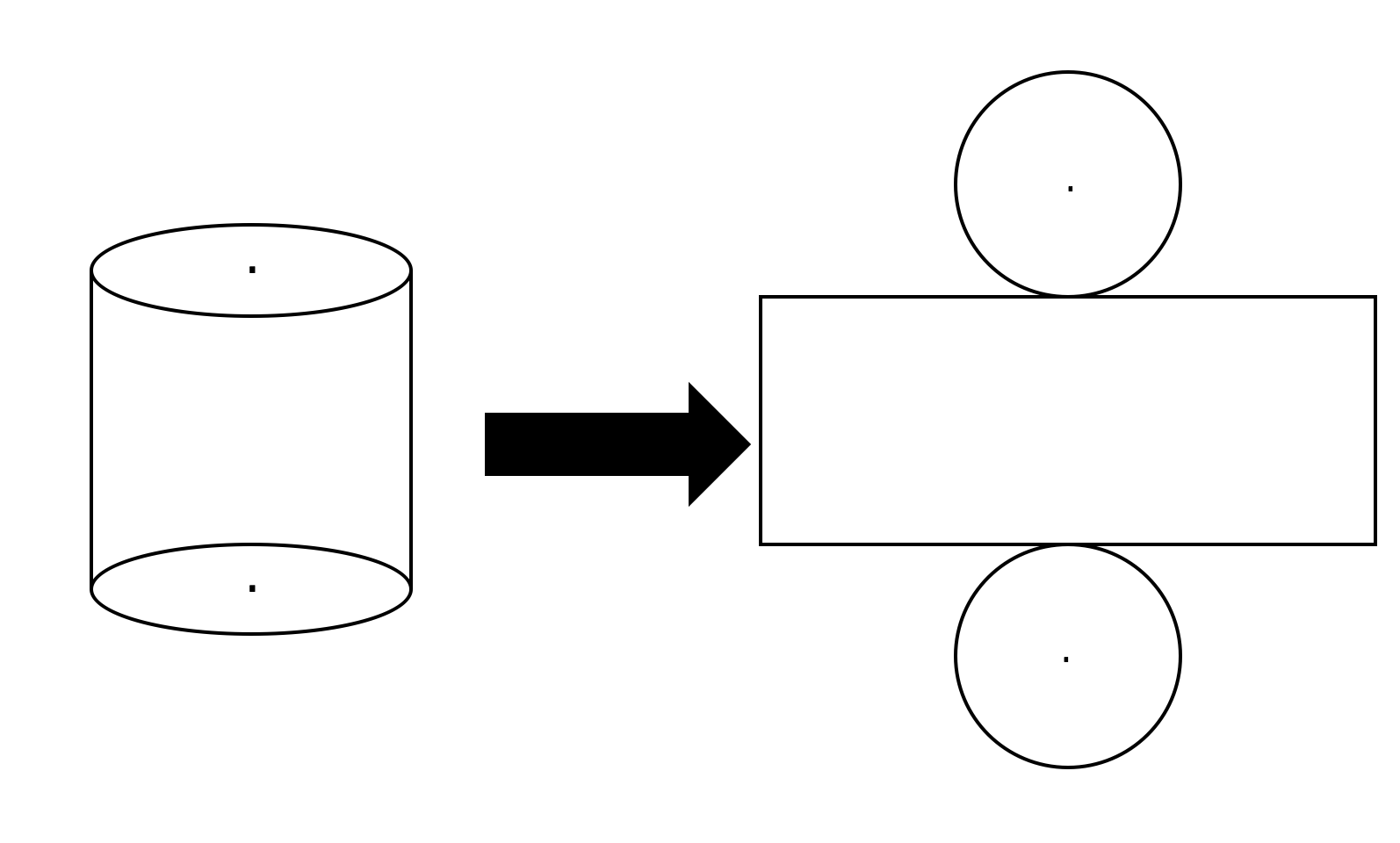



3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ



Updated 立方体の表面積計算電卓アプリ Pc Iphone Ipad App Mod Download 21




円錐と円柱の表面積を簡単に求める方法 Easy Way To Find The Surface Area Of Cones And Cylinders Youtube
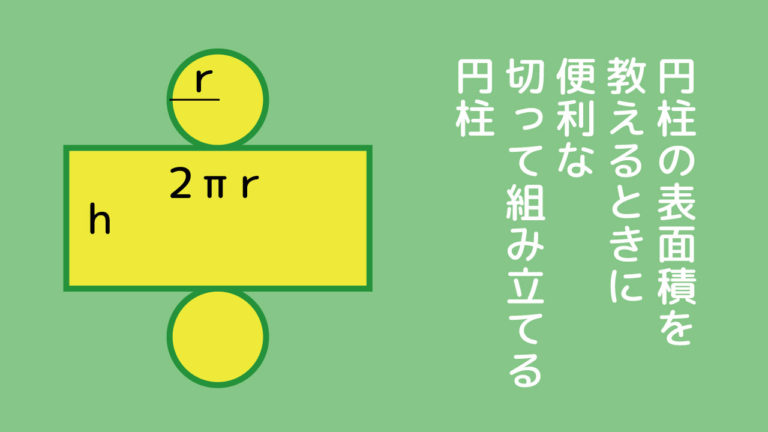



中1数学 円柱の表面積を教えるときに役立つ展開図 数学検定5級




円柱の表面積 Youtube




角柱や円柱の表面積の求め方を教えてください Clear




Nitter




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




はりねずみ 𝑎 𝑎 は数学の先生 ちなみにこれがなんで成り立つのか最後までよくわからなかった 結果的にそうなるだけなの カバリエリの原理みたいに普遍的な原理があるの 一方で球の表面積 が円柱の表面積の2 3倍ってのもなかなかきれいなんだけど



高校入試 英語 数学 学習 立体の表面積と体積
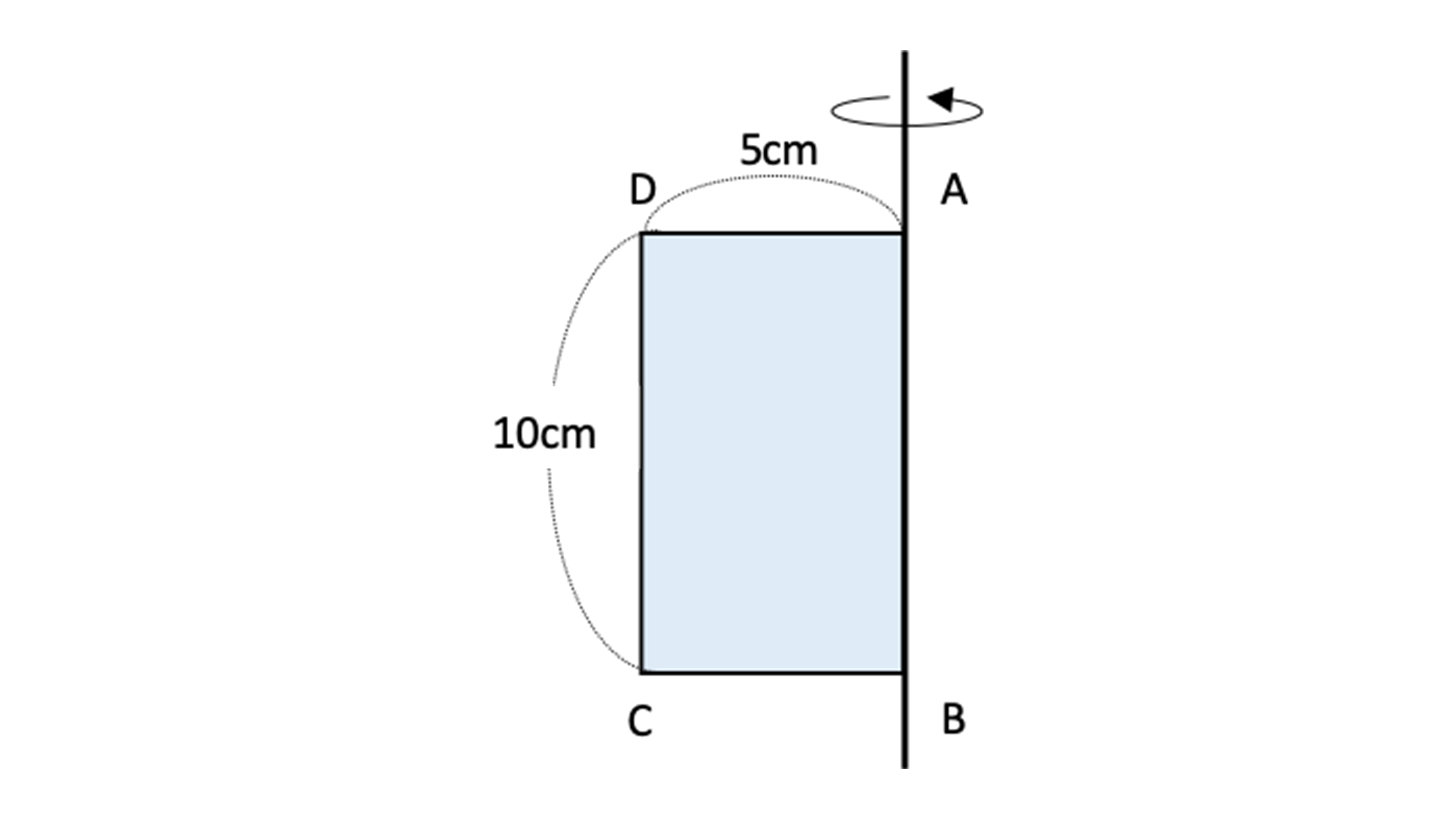



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱を半分に切った形の体積と表面積を求めよ 解き方と答えを教えて下さい Clear



Nitter Allella




2 を途中式を含めて教えてください Clear



立体 の 表面積 求め 方




円柱の表面積の求め方 公式と計算例




Easy Way To Find The Surface Area Of A Cylinder Youtube




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




球の表面積と体積の公式 数学fun




中学1年生 数学 無料問題集 角柱や円柱の表面積 おかわりドリル



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



1



立方体の表面積計算電卓アプリ Iphone Ipad Game Reviews Appspy Com



Updated 立方体の表面積計算電卓アプリ For Pc Mac Windows 7 8 10 Free Download 21




初等幾何 球の表面積を求める 大人が学び直す数学



Math 円柱 内接する球 円錐の体積と表面積 働きアリ




円柱の表面積と体積を求める公式 具体例で学ぶ数学



3




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト



0 件のコメント:
コメントを投稿